Elektronický vzdelávací materiál

Parametrická rovnica roviny

Rovina je určená troma nekolineárnymi bodmi, resp. bodom a dvoma lineárne nezávislými vektromi.

Zvoľ'me v rovine bod A[a₁; a₂; a₃] a dva lineárne nezávislé vektory u = [u₁; u₂; u₃] v = [₁; v₂; v₃]

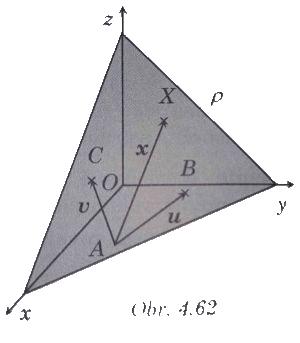
Potom každý bod X roviny pje súč-tom bodu A a vektora x, ktorý je li-neárnou kombináciou vektorov u, v, teda
X ∈ ρ ⇔ X = A + x ; X = A + ru + sv, r, s ∈ R

Každému bodu X roviny ρ sú teda priradené dve reálne čísla r a s tak, že X = A + ru + sv. Čísla r a s priradené bodu X sú parametre bodu X.
Rovnica X = A + ru + su, r, s∈ R, sa nazýva parametrická rovnica roviny ρ. Môžeme ju rozpísať do súradníc:

ρ: x = a₁ + r * u₁+ s * v₁
y = a₂ + r * u₂+ s * v₂

z = a₃ + r * u₃+ s * v₃